One thing that I find very irritating is when one of my students leaves the cap off of a dry erase marker. This happened a couple of weeks ago, and to illustrate how deeply it bothers me, I had a funeral service at the beginning of each of my classes. Standing next to a grave of dead markers (which is basically a box with a foam tombstone attached), I said the following:
"I regret to inform you that this morning, at approximately 7:40 A.M, I entered the classroom and noticed that the cap on Black Dry-Erase Low Odor Chiseled Tip Expo Marker was not firmly attached. I feared the worst, rushed over to Black Dry-Erase Low Odor Chiseled Tip Expo Marker, picked it up, and attempted to draw a squiggle on the board. Alas, nothing came out. Black Dry-Erase Low Odor Chiseled Tip Expo Marker's life force was depleted.
Today, we honor the life of Black Dry-Erase Low Odor Chiseled Tip Expo Marker. No, you weren't perfect. Mistakes were made. But, you were a bold marker. You helped us solve the most difficult of math problems. It seems like just yesterday we were writing the one-hour delay bell schedule on the board.
You were taken from this world too soon. Your last act was to write "Hi Mr Kraft" on the board with a smiley face underneath. Little did I know, that you were really saying good-bye. I will miss you Black Dry-Erase Low Odor Chiseled Tip Expo Marker. Say "hi" to Red for us."
---------------------------------
Here is a picture of Vigo the Carpathian from Ghostbusters II. Some of my students find this poster disturbing. I don't know why.
"Death is but a door. Time is but a window. I'll be back." -Vigo, the Carpathian
Sunday, October 6, 2013
Sunday, August 11, 2013
51 Days til Halloween?
I really like the following activity and I've blogged about it here.
Which is why I got really excited when I saw this Halloween decoration the other day at Michael's:
You can display this decoration 51 days before Halloween! Or can you?
What if this decoration can't display each number between 1 and 51? Would that constitute as some sort of false advertising?
Sunday, August 4, 2013
TMC13 Recap - (Where I basically just talk about people behind their backs.)
This was supposed to be a recap of cool things I learned at Twitter Math Camp 2013 (TMC13). But then I thought, the hell with you people. You should have been there. It's your fault that you don't know what happened. Why should I fill you in on every little thing? Let this be a lesson to you. Next time, you can get yourself off of that damn couch and attend a conference.
Alright. Maybe your lameness can be blamed on having a horrible childhood. Or maybe you're too poor to make the trip. I guess I can cut you some slack.
I'm not going to give a detailed description of presentations I attended. There are already a lot of people already doing that. To me, the coolest thing about this conference is meeting all of the people I've been following in blogs and on twitter. These people have had an amazing impact on who I am as a teacher. I couldn't pass up the opportunity to meet them, exchange more ideas, and have some fun in the process. So this is basically an homage to those I've met and how awesome they are.
Every year I try to achieve some sort of ideal in my practices. Fawn Nguyen epitomizes what that ideal should be. I don't know anyone who blogs as honestly or as intelligently as she does. She is obviously an amazing teacher and I strive to be just like her...just taller and less Vietnamese. She did a presentation on Conway's Rational Tangles.
John Berray is another great teacher, which I didn't really realize until I attended his session this year at TMC. He is obviously a great performer in the classroom and I have to believe that his students adore him. He does this great activity called Shot at the Glory. Check it out.
John also taught us the best way to open bananas. (This isn't him in the video.) I tried it out this morning and it works like a charm.
I met Max Ray during the EnCoMPASS fellowship and was impressed by his notice/wonder talk. He has such a natural sense of humor and I could just listen to him talk about anything. He's also written a book which will be out very soon. I'm so excited to read it! (He also gave me free passes for me and my son to use at the Elmwood Park Zoo. Nice guy.)
Michael Pershan is probably one of the most reflective teachers I've met. I envy his curiosity and enjoy reading and listening to his thoughts. And the highlight of my trip has to be his performance of "99 Problems" at karaoke. I don't think anyone was expecting that.
Ashli Black impresses me how she is able to immerse herself in this strange mathy world of ours, traveling to anything and everything including PCMI. I attended her presentation on building algebraic thinking. It was a great hands-on activity that can spark a lot of great conversation in the classroom. I also have to give her a shout out for suggesting I read Embedded Formative Assessment. The research on feedback is very surprising.
Lisa Henry did an amazing job on organizing all of this and I can't thank her (and her husband) enough for doing it. I'd also like to thank her husband for not punching me in the face after I sang "Paradise by the Dashboard Light" with his wife.
It was cool meeting Nik Doran, because he's British and I've been watching a lot of British TV lately: Doctor Who and Sherlock. He's no Benedict Cumberbatch, so I closed my eyes and pretended he was. (What? No. I'm not in love with Benedict Cumberbatch. I mean, yeah, he's incredibly handsome and quirky. But love? No. I mean, I like him. Let's change the subject. This is making me uncomfortable.) I'm also impressed with how he's trying to bring this weird twitterblogosphere thing to the UK.
Sadie Estrella is full of piss and vinegar, which is a testament to how passionate she is about life and teaching. I also think she could beat me up.
Chris Robinson is a great resource who also lives in Pennsylvania. I'm always impressed with the amount of time he gives to this math community. It was nice to share our aggravations over how stupid Pennsylvania is being over their implementation (or non-implementation) of the Common Core Standards.
Eli Luberoff is the founder of desmos.com and gave a great presentation of his software. I've never seen math teachers get so excited over software features. He's also a really nice guy who is genuinely interested in how people are using desmos and how he can improve it for them.
Jen Silverman threw a cardboard dodecahedron at my face as I was trying to drink my coffee.
Christopher Danielson is a very insightful guy and I love his lessons on food (Oreos and Tootsies) and his conversations with his children. He gave a great presentation on the two of the Five Practices for Orchestrating Productive Mathematics Discussions: anticipation and connecting. We were asked to see how many ways we could cut a tootsie roll into four equal pieces. I came up with the following solution, which I wasn't sure about at first, but it works. It's just weird because the four pieces don't have the same shape.
Mark Sanford is starting his first year of teaching. I think it's incredibly awesome that he has tapped into this community before his teaching career has even started. He is so lucky to have so much great direction from the get-go.
The Mathalcious team is basically the Justice League of math education. Karim knows how to find talent (Chris Lusto, Ginny Stuckey, Matt Lane, Kate Nowak), and I am continually impressed by what he and his team have produced. I am also grateful to now have an understanding of the "romance cone" which is a graphical way of representing the dating rule of "half your age plus 7".
Sean Sweeney, Rachel Kernodle, Julie Reulbach, Kate Nowak, Chris Lusto and Greg (something or other) did a great job ending the conference with a parody of Tik-Tok by Kesha. At the last minute, they asked me to go up on stage with them and dance, but I'm glad I didn't. It was too much fun to watch.
Greg (in the video above) gave a quick talk on how he uses his ukelele to teach students. Apparently, when students are working and he is playing his ukelele, the students think that he is too busy to be bothered, so they look to each other for help. He still walks around the room and monitors their progress, but he is no longer a crutch for the students. Genius.
Julie Reulbach (also in the video above) always has an infectious smile on her face and is perpetually happy. I'm so glad that I got to know her a little better.
Kate Nowak (also in the video above) had a great t-shirt with the following image. Kate also asked me to sing Van Halen's Hot for Teacher at karaoke. How could I refuse?
Shauna Hedgepeth gave a great presentation on some of the activities she does with her statistics classes. The coolest part was that I'm able to take any of those ideas and use them in a middle school classroom. She also had us running up stairs to find our horsepower.
Steve Leinwand has a loud booming voice, which fits him because he seems like the authority on mathematics education. I'm still impressed that he came to the conference which shows just how cool and involved he is.
Sam Shah is a lovable guy and fun to hang out with. I was a little worried that I offended him because I told him that I did not enjoy watching Real Housewives of...Wherever, but I think he's forgiven me. I'm so glad that I got to spend some time with him my last night there. He taught us how to play a really cool word game called Contact.
And what did I provide in return for all of their awesomeness? My amazing dance moves!
Late Additions:
Sophie Germain! I mean Anne Schwartz! Or whatever her name is! That girl was awesome at karaoke night and she did a great little talk about how people need to shut up and listen to students. (We have a tendency to cut people off and try to fix their problems for them.) She's another person I regret not getting to know better.
Alright. Maybe your lameness can be blamed on having a horrible childhood. Or maybe you're too poor to make the trip. I guess I can cut you some slack.
I'm not going to give a detailed description of presentations I attended. There are already a lot of people already doing that. To me, the coolest thing about this conference is meeting all of the people I've been following in blogs and on twitter. These people have had an amazing impact on who I am as a teacher. I couldn't pass up the opportunity to meet them, exchange more ideas, and have some fun in the process. So this is basically an homage to those I've met and how awesome they are.
Every year I try to achieve some sort of ideal in my practices. Fawn Nguyen epitomizes what that ideal should be. I don't know anyone who blogs as honestly or as intelligently as she does. She is obviously an amazing teacher and I strive to be just like her...just taller and less Vietnamese. She did a presentation on Conway's Rational Tangles.
John Berray is another great teacher, which I didn't really realize until I attended his session this year at TMC. He is obviously a great performer in the classroom and I have to believe that his students adore him. He does this great activity called Shot at the Glory. Check it out.
John also taught us the best way to open bananas. (This isn't him in the video.) I tried it out this morning and it works like a charm.
I met Max Ray during the EnCoMPASS fellowship and was impressed by his notice/wonder talk. He has such a natural sense of humor and I could just listen to him talk about anything. He's also written a book which will be out very soon. I'm so excited to read it! (He also gave me free passes for me and my son to use at the Elmwood Park Zoo. Nice guy.)
Michael Pershan is probably one of the most reflective teachers I've met. I envy his curiosity and enjoy reading and listening to his thoughts. And the highlight of my trip has to be his performance of "99 Problems" at karaoke. I don't think anyone was expecting that.
Ashli Black impresses me how she is able to immerse herself in this strange mathy world of ours, traveling to anything and everything including PCMI. I attended her presentation on building algebraic thinking. It was a great hands-on activity that can spark a lot of great conversation in the classroom. I also have to give her a shout out for suggesting I read Embedded Formative Assessment. The research on feedback is very surprising.
Lisa Henry did an amazing job on organizing all of this and I can't thank her (and her husband) enough for doing it. I'd also like to thank her husband for not punching me in the face after I sang "Paradise by the Dashboard Light" with his wife.
It was cool meeting Nik Doran, because he's British and I've been watching a lot of British TV lately: Doctor Who and Sherlock. He's no Benedict Cumberbatch, so I closed my eyes and pretended he was. (What? No. I'm not in love with Benedict Cumberbatch. I mean, yeah, he's incredibly handsome and quirky. But love? No. I mean, I like him. Let's change the subject. This is making me uncomfortable.) I'm also impressed with how he's trying to bring this weird twitterblogosphere thing to the UK.
Sadie Estrella is full of piss and vinegar, which is a testament to how passionate she is about life and teaching. I also think she could beat me up.
Chris Robinson is a great resource who also lives in Pennsylvania. I'm always impressed with the amount of time he gives to this math community. It was nice to share our aggravations over how stupid Pennsylvania is being over their implementation (or non-implementation) of the Common Core Standards.
Eli Luberoff is the founder of desmos.com and gave a great presentation of his software. I've never seen math teachers get so excited over software features. He's also a really nice guy who is genuinely interested in how people are using desmos and how he can improve it for them.
Jen Silverman threw a cardboard dodecahedron at my face as I was trying to drink my coffee.
Christopher Danielson is a very insightful guy and I love his lessons on food (Oreos and Tootsies) and his conversations with his children. He gave a great presentation on the two of the Five Practices for Orchestrating Productive Mathematics Discussions: anticipation and connecting. We were asked to see how many ways we could cut a tootsie roll into four equal pieces. I came up with the following solution, which I wasn't sure about at first, but it works. It's just weird because the four pieces don't have the same shape.
Mark Sanford is starting his first year of teaching. I think it's incredibly awesome that he has tapped into this community before his teaching career has even started. He is so lucky to have so much great direction from the get-go.
The Mathalcious team is basically the Justice League of math education. Karim knows how to find talent (Chris Lusto, Ginny Stuckey, Matt Lane, Kate Nowak), and I am continually impressed by what he and his team have produced. I am also grateful to now have an understanding of the "romance cone" which is a graphical way of representing the dating rule of "half your age plus 7".
Sean Sweeney, Rachel Kernodle, Julie Reulbach, Kate Nowak, Chris Lusto and Greg (something or other) did a great job ending the conference with a parody of Tik-Tok by Kesha. At the last minute, they asked me to go up on stage with them and dance, but I'm glad I didn't. It was too much fun to watch.
Greg (in the video above) gave a quick talk on how he uses his ukelele to teach students. Apparently, when students are working and he is playing his ukelele, the students think that he is too busy to be bothered, so they look to each other for help. He still walks around the room and monitors their progress, but he is no longer a crutch for the students. Genius.
Julie Reulbach (also in the video above) always has an infectious smile on her face and is perpetually happy. I'm so glad that I got to know her a little better.
Kate Nowak (also in the video above) had a great t-shirt with the following image. Kate also asked me to sing Van Halen's Hot for Teacher at karaoke. How could I refuse?
Shauna Hedgepeth gave a great presentation on some of the activities she does with her statistics classes. The coolest part was that I'm able to take any of those ideas and use them in a middle school classroom. She also had us running up stairs to find our horsepower.
Steve Leinwand has a loud booming voice, which fits him because he seems like the authority on mathematics education. I'm still impressed that he came to the conference which shows just how cool and involved he is.
Sam Shah is a lovable guy and fun to hang out with. I was a little worried that I offended him because I told him that I did not enjoy watching Real Housewives of...Wherever, but I think he's forgiven me. I'm so glad that I got to spend some time with him my last night there. He taught us how to play a really cool word game called Contact.
And what did I provide in return for all of their awesomeness? My amazing dance moves!
Late Additions:
Sophie Germain! I mean Anne Schwartz! Or whatever her name is! That girl was awesome at karaoke night and she did a great little talk about how people need to shut up and listen to students. (We have a tendency to cut people off and try to fix their problems for them.) She's another person I regret not getting to know better.
Wednesday, July 3, 2013
Whiteboard Envy
My whiteboards are small. And this bothers me, because I know other teachers (Andrew and Fawn) have bigger whiteboards and they're able to do so much more with them. They know how insecure I am, but that doesn't stop them from showing off.
So I decided to write a letter to my administration this morning. I hope that I was convincing.
Update:
Everyone in the twitterverse (and their mothers) is telling me that I should just go to Lowes or Home Depot:
Finally, Dan Bowdoin had this solution....
So I decided to write a letter to my administration this morning. I hope that I was convincing.
Ladies and gentlemen,
First off, let me tell you how impressed I am with your
charming personalities and insights. You are all very in tune with what works
in education, and very supportive of teachers’ requests for new materials.
Incidentally, I have been having some enlightening
discussions with some other successful teachers from across the country, and a
common theme in group problem-solving is the use of large whiteboards. In my
own experiences, a whiteboard seems to have some magical effect on student
engagement. Could it be that a clean whiteboard, this blank slate, represents
new beginnings and unlimited possibilities? Could it be that students are
better at sharing their work when they share their workspace? Do some of my
students enjoy the pleasant aromas emanating from their dry-erase markers? (The
answer to this is a resounding “Yes!”. One student in particular prefers the
black markers because they smell like bananas.) Regardless, it seems that
whiteboarding is a preferable medium for students to share their mathematical
thinking.
But alas…I do not possess whiteboards of such size that
would foster such thinking. My tiny 12” by 12” boards are capable of containing
only the smallest amount of information. They are woefully inadequate.
This is why I would like to purchase large, group-friendly,
24” by 32” whiteboards from http://www.whiteboardsusa.com/.
Each board costs only $10.50, or the cost of two Pomegranate Frappaccinos.
Accounting for the fact that I could have a class of 30 students, and the
smallest group I might have is a group of two students, it would make sense
that we order 15 boards for a cost of $157.50. There would also be some
shipping costs, which might be costly, but isn’t it worth it…you know, for the
kids?
Thank you for taking the time to consider this purchase.
Nathan Kraft
Math Department
DHH Lengel Middle School, Pottsville, PA
Class Website: mrkraft.wikispaces.com
Blog: nathankraft.blogspot.comUpdate:
Everyone in the twitterverse (and their mothers) is telling me that I should just go to Lowes or Home Depot:
@nathankraft1 @fawnpnguyen @mr_stadel @fnoschese just curious, but why not go to lowes and the school buy multiple class sets for same $?
— Dan Anderson (@dandersod) July 3, 2013
@nathankraft1 @fawnpnguyen @mr_stadel Do you have a Home Depot or Lowes nearby? They can cut a large sheet of tileboard to spec.
— Frank Noschese (@fnoschese) July 3, 2013
@fnoschese @nathankraft1 I went to Lowes. Much cheaper...probably a third the cost.I think the biggest concern I have about this is that the edges will be rough which does not look pretty and could give kids splinters. Yeah, I could sand it down...would that be sufficient? I also am concerned about the thickness and quality of the materials. I don't want these things breaking easily. Any thoughts from you, the whiteboarding community?
— Lois Burke (@lbburke) July 3, 2013
Finally, Dan Bowdoin had this solution....
@nathankraft1 HD cut these and then I taped them. Lasted all year! #edges @fawnpnguyen @mr_stadel @fnoschese pic.twitter.com/eqUn4fp5TL
— Dan Bowdoin (@danbowdoin) July 3, 2013
Sunday, June 30, 2013
The Oasis of Troy
This past week I spent some time in Philadelphia for the EnCoMPASS Project (more on that later). During the last day, Fawn and I were walking downtown and stopped at this fountain near city hall.
There we met a man named Troy who was selling bottled water. He sat comfortably in the shade of a tree and called out to people as they walked by, "Excuse me, would you like some water?" Although it was a warm day and plenty of people were in the park, it didn't seem to me that he was selling much. This probably had more to do with the fact that people don't like to be bothered by random vendors on the street. I'm one of those people, so I could certainly sympathize with them. Or maybe they just didn't want water.
Eventually a couple walked by, and as per usual, Troy asked if they would like some water. The man said "no". Troy followed up with, "perhaps your lady is thirsty?", and without hesitation, the man again said "no". Troy turned to us and said, "he didn't even ask her!" Fawn and I lost it and Troy joked with us about how the girl was likely to start an argument with her boyfriend for not offering her some water.
In order for Troy to increase sales, I made a suggestion. Troy needed to market his product better. People had to see his corner of the park as a refuge from the hot sun...an oasis. The Oasis of Troy!
As the next customer walked by, Troy, who had not sold any bottles for quite some time said, "Welcome to my oasis! Would you like some water?" And sure enough, the man stopped, seemed to think about it for a second, and said, "Yes."
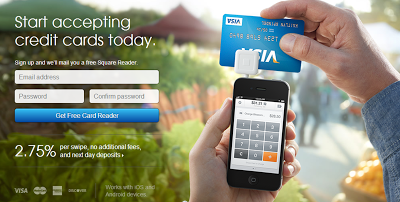
Later, it came up that Fawn and I are math teachers, and Troy became very excited. Aside from selling water, he also sells credit card processors to businesses. He explained that his main competition in credit card processing is something called The Square.
The Square charges 2.75% per credit card swipe with no additional fees. Troy charges 1.09% per swipe with a $10 monthly charge. He explained that he wasn't having much success and that many businesses turned him away, thinking that the monthly fee was too high. But he was convinced that his processor was cheaper. He just didn't know how to express it. There was probably a formula to show this, but he didn't know what it was.
After some discussion with Fawn, we came up with the following formulas:
s = 0.0275x
t = 0.0109x + 10
x is the monthly revenue, s represents the fees charged by The Square, and t represents the fees charged by Troy.
After setting The Square's charges equal to Troy's, we found that the break-even point was about $600. This seemed to be good news for Troy, because if a business takes in more than $600 in revenue, Troy's processor is cheaper. And sure, he looks worse for a revenue less than $600, but any business that takes in less than $600 per month will certainly go out of business.
I asked Troy, what do I say to students who ask, "when would I ever use this?" He said to tell them, "No, you are never going to use this, but knowing it will allow you to do the things that you want to do." Well said.
Update:
For those of you who know Fawn, you know she solves just about every math problem with rectangles. It's uncanny. Here's her solution:
Eventually a couple walked by, and as per usual, Troy asked if they would like some water. The man said "no". Troy followed up with, "perhaps your lady is thirsty?", and without hesitation, the man again said "no". Troy turned to us and said, "he didn't even ask her!" Fawn and I lost it and Troy joked with us about how the girl was likely to start an argument with her boyfriend for not offering her some water.
In order for Troy to increase sales, I made a suggestion. Troy needed to market his product better. People had to see his corner of the park as a refuge from the hot sun...an oasis. The Oasis of Troy!
As the next customer walked by, Troy, who had not sold any bottles for quite some time said, "Welcome to my oasis! Would you like some water?" And sure enough, the man stopped, seemed to think about it for a second, and said, "Yes."
Later, it came up that Fawn and I are math teachers, and Troy became very excited. Aside from selling water, he also sells credit card processors to businesses. He explained that his main competition in credit card processing is something called The Square.
The Square charges 2.75% per credit card swipe with no additional fees. Troy charges 1.09% per swipe with a $10 monthly charge. He explained that he wasn't having much success and that many businesses turned him away, thinking that the monthly fee was too high. But he was convinced that his processor was cheaper. He just didn't know how to express it. There was probably a formula to show this, but he didn't know what it was.
After some discussion with Fawn, we came up with the following formulas:
s = 0.0275x
t = 0.0109x + 10
x is the monthly revenue, s represents the fees charged by The Square, and t represents the fees charged by Troy.
After setting The Square's charges equal to Troy's, we found that the break-even point was about $600. This seemed to be good news for Troy, because if a business takes in more than $600 in revenue, Troy's processor is cheaper. And sure, he looks worse for a revenue less than $600, but any business that takes in less than $600 per month will certainly go out of business.
I asked Troy, what do I say to students who ask, "when would I ever use this?" He said to tell them, "No, you are never going to use this, but knowing it will allow you to do the things that you want to do." Well said.
Update:
For those of you who know Fawn, you know she solves just about every math problem with rectangles. It's uncanny. Here's her solution:
Torturing Kids with Toothpicks - Part 4
If you've been following my blog, you probably know about my adventures with toothpicks. Basically I placed a bunch of them on my classroom floor for a math problem. I only realized this morning that I never showed the final product on my blog...just on my wikispace. You can find all of that work here:
http://mrkraft.wikispaces.com/Triangle+of+Toothpicks
While I received a little bit of feedback from the twitter crowd, I'd appreciate more. Any ideas on presentation? How would you use this in your classroom? What modifications would you make? Any kind of extension ideas?
Thanks!
Incidentally, a couple of weeks ago I made a change to my Three Act page. It wasn't visually appealing (all text) and I thought I could do better. Click here for the new page.
Saturday, May 25, 2013
Torturing Kids with Toothpicks - Part 3
Here is the first act of my toothpick lesson. Feedback is appreciated.
Here is part 1 and part 2 of this series.
Here is part 1 and part 2 of this series.
Thursday, May 23, 2013
Sometimes I Dance
This has nothing to do with math, but sometimes I dance. (I'm the one wearing the vest.)
Sunday, May 19, 2013
Give Me the Wrong Answer
The other day I had the following warm-up on the board:
It takes 8 elephants 8 minutes to drink 8 pints of water. If they drink at the same rate, how many elephants would you need to drink 16 pints of water in 16 minutes?
(What is it with me and elephants?)

This isn't a difficult problem if you take the time to think about it. But as I walked around the room, I saw quite a few students had it wrong. Some students were thinking proportions and assumed that the number of elephants would also double. Some students noticed that 16 was evenly divisible by 8 and wrote 2 elephants. (As if I would give them something that easy.) And some had the correct answer of 8.
So after walking around, I asked, "How many elephants?" And not surprisingly, not many hands went up. Even the students who had 8 seemed to be a bit reserved.
For me, it's a little disappointing because I've had these kids all year and I would hope that at this point I could get a little more participation out of them. Obviously some students are still not very confident and don't like putting themselves out there in front of their classmates.
When this happens, I try a different approach. After seeing that only a few hands were raised, I said, "Wait. I didn't mean to ask that. Let me try again. What do you think is a common wrong answer?"
Then, a beautiful thing happened. About half the class had their hands raised. Many of these students did not know the right answer, but at some point during the process, they figured out what wasn't right. These students now felt like they had something worthwhile to contribute and were more comfortable in becoming a part of the discussion.
A student gave one of the incorrect answers I was looking for. I asked, "Why is it wrong?" She said something about rates not being the same (1 pint per 8 minutes versus 1 pint per 16 minutes). Using that, I follow up with, "Many of you thought that it would only take 2 elephants. Can someone explain why that doesn't work either?"
More hands went up.
Finally, I asked my original question, "So how many elephants?" At this point, many more students were ready to share. The students that had it wrong fixed their mistakes. The students that were right in the first place were more confident in their answers and willing to share.
On a related note: I always hate those pictures in educational magazines that show a smiling teacher in the front of a classroom, filled with students, all of whom have their hands raised high in the air. Why do I get the feeling that these pictures are all staged with the photographer telling the kids, "OK everybody! Pretend to be really excited about class today and put your hands high in the air!" I find this photo to be especially irritating because A) there's no way those kids are old enough to be learning about quadratic equations and B) no teacher would let their students have bottles of water on their desks. Someone would be asking to go the bathroom every five minutes!
It takes 8 elephants 8 minutes to drink 8 pints of water. If they drink at the same rate, how many elephants would you need to drink 16 pints of water in 16 minutes?
(What is it with me and elephants?)

This isn't a difficult problem if you take the time to think about it. But as I walked around the room, I saw quite a few students had it wrong. Some students were thinking proportions and assumed that the number of elephants would also double. Some students noticed that 16 was evenly divisible by 8 and wrote 2 elephants. (As if I would give them something that easy.) And some had the correct answer of 8.
So after walking around, I asked, "How many elephants?" And not surprisingly, not many hands went up. Even the students who had 8 seemed to be a bit reserved.
For me, it's a little disappointing because I've had these kids all year and I would hope that at this point I could get a little more participation out of them. Obviously some students are still not very confident and don't like putting themselves out there in front of their classmates.
When this happens, I try a different approach. After seeing that only a few hands were raised, I said, "Wait. I didn't mean to ask that. Let me try again. What do you think is a common wrong answer?"
Then, a beautiful thing happened. About half the class had their hands raised. Many of these students did not know the right answer, but at some point during the process, they figured out what wasn't right. These students now felt like they had something worthwhile to contribute and were more comfortable in becoming a part of the discussion.
A student gave one of the incorrect answers I was looking for. I asked, "Why is it wrong?" She said something about rates not being the same (1 pint per 8 minutes versus 1 pint per 16 minutes). Using that, I follow up with, "Many of you thought that it would only take 2 elephants. Can someone explain why that doesn't work either?"
More hands went up.
Finally, I asked my original question, "So how many elephants?" At this point, many more students were ready to share. The students that had it wrong fixed their mistakes. The students that were right in the first place were more confident in their answers and willing to share.
Wednesday, May 15, 2013
I Shall Never Play a Review Game Again!
Update 8/3/15: I've decided that you probably shouldn't use this game in class and I blogged about that here. I could just delete this post, but I figure there's always the chance that someone will think of a way to improve it.
This is the second part of my ramblings about exponents. You should probably go read the first part before you read this!
I don't think there was ever a moment in my life where I said, "Hey! That review game worked really well today. It really helped to prepare my students for that big test tomorrow. Everyone was fully engaged and asking questions about the problems they didn't understand. They had so much fun and I was really impressed by their good sportsmanship! I can't wait to do it again."
Here's why it never worked for me.... The kids who struggle don't want others to notice, so they make some excuse about how they don't want to play the game. The game is "stupid". So I have to give them a worksheet to do instead. Then somebody notices somebody cheating and demands that points be taken away. Then I have to explain that I didn't catch them, but I will certainly be watching to see if anyone is cheating from now on. Then someone will get caught, and I take points away from that team, and then that team gets mad, and then the other team says something nasty to them, and then they say something nasty back, and then I explain that it's just a game, but that doesn't help, because after a few questions they're arguing again, and then I threaten to give them all boring worksheets to do, and so on and so forth.
I don't know. Maybe I'm doing something wrong, but my kids can't seem to handle competition.
So after one horrible day, I declared, "I shall never play another review game again!" That sounds overly dramatic, but that's how it went down.
So today, after seven months of not allowing any games, I decided to play a game.
It was very spontaneous. Someone asked if we could "do something fun", which annoys me to no end, but after practicing solving systems for the last couple of days, I agreed that something fun was in order. I also ran out of Oreos from a task we did the other day, so bribing them to do work was out of the question.
I remembered reading a post a few months back by Kara Wilkins called Grudgeball. It was some sort of game where everybody gets so many X's and you want to be the last student/group with an X. Kids take turns answering questions, and if the question is right, they toss a basketball into a hoop, and if they make a shot, they can erase one of their opponent's X's. I basically did the same thing, minus the basketball. (I decided to name it "Grudge"...but there has to be a better name for it.)
I wrote everyone's names on the Smartboard and everybody got three X's. It looked something like this:
If you remember, I said I'd never play a review game again. And technically, I didn't. This wasn't a review. This was mostly new material. I wasn't using a game to trick my students into practicing something one last time before a test. I was using a game to encourage them to learn something new.
Caution: This game seems to work differently for different groups of kids. If there's a lot of animosity in the room, it's probably not a good idea.
This is the second part of my ramblings about exponents. You should probably go read the first part before you read this!
I don't think there was ever a moment in my life where I said, "Hey! That review game worked really well today. It really helped to prepare my students for that big test tomorrow. Everyone was fully engaged and asking questions about the problems they didn't understand. They had so much fun and I was really impressed by their good sportsmanship! I can't wait to do it again."
Here's why it never worked for me.... The kids who struggle don't want others to notice, so they make some excuse about how they don't want to play the game. The game is "stupid". So I have to give them a worksheet to do instead. Then somebody notices somebody cheating and demands that points be taken away. Then I have to explain that I didn't catch them, but I will certainly be watching to see if anyone is cheating from now on. Then someone will get caught, and I take points away from that team, and then that team gets mad, and then the other team says something nasty to them, and then they say something nasty back, and then I explain that it's just a game, but that doesn't help, because after a few questions they're arguing again, and then I threaten to give them all boring worksheets to do, and so on and so forth.
I don't know. Maybe I'm doing something wrong, but my kids can't seem to handle competition.
So after one horrible day, I declared, "I shall never play another review game again!" That sounds overly dramatic, but that's how it went down.
So today, after seven months of not allowing any games, I decided to play a game.
It was very spontaneous. Someone asked if we could "do something fun", which annoys me to no end, but after practicing solving systems for the last couple of days, I agreed that something fun was in order. I also ran out of Oreos from a task we did the other day, so bribing them to do work was out of the question.
I remembered reading a post a few months back by Kara Wilkins called Grudgeball. It was some sort of game where everybody gets so many X's and you want to be the last student/group with an X. Kids take turns answering questions, and if the question is right, they toss a basketball into a hoop, and if they make a shot, they can erase one of their opponent's X's. I basically did the same thing, minus the basketball. (I decided to name it "Grudge"...but there has to be a better name for it.)
I wrote everyone's names on the Smartboard and everybody got three X's. It looked something like this:
(I know what you're thinking...does he really have kids named Fawn? Hedge? Timon? Bowman??? No. They're completely made up. No one would actually name their kids that.)
I then explained the rules of the game to my students. An expression with exponents would be written on the board. Everyone would write an answer on their little whiteboards, and then anyone with a right answer would erase one X from the board. The last student with an X under their name wins.
First problem:
This isn't tough. In fact, they just learned how to expand these expressions and rewrite them yesterday. So everybody got it right. Awesome. And everybody got to remove an X. Our board looked like this:
Monya, Kishi and Andrew took Fawn out pretty quickly. Fawn took a little bit of revenge on Andrew, but it didn't do much good.
I gave the students another problem, but this time it was something a little different.
Several of my students point out that they've never seen a problem like this before. With the utmost seriousness, I said, "No. You've never seen this. But you're smart enough to figure it out. Just think about what's going on here." It was just one of those moments where you tell the kids that they're on their own and they need to believe in themselves. Maybe a little corny, but it works.
A little over half of the class got the right answer. We talked about what people did to simplify the expression, and for the most part, everyone was engaged because they wanted to make sure they were good at playing the game. And if that's the carrot that I have to dangle to get my students to think algebraically with 11 days left in the school year, so be it.
Note on game play: Although Fawn, Hedge, and Nathan were out of the game, they could play a zombie role and "attack" other players by erasing their X's. This motivated them to keep playing, even though they could no longer win.
Another problem was given that was similar to the last one. That time just about everybody got it. Then we tried dividing powers. Only two or three students figured it out. Then we did another, then half the class figured it out. You see where I'm going with this?
I kept introducing something new. Some students got it right away. For some, it took a couple tries. But eventually, everybody learned how to do it.
The game was finished when all of the X's were gone except for one. Usually the kid that wins is the one you least expect.
If you remember, I said I'd never play a review game again. And technically, I didn't. This wasn't a review. This was mostly new material. I wasn't using a game to trick my students into practicing something one last time before a test. I was using a game to encourage them to learn something new.
Caution: This game seems to work differently for different groups of kids. If there's a lot of animosity in the room, it's probably not a good idea.
Exponents Rules are Lame.
I originally wrote one long post about teaching exponents and incorporating a game. It got to be so long that I split it up into two posts. So bear with me.
Admit it. For most students, exponent rules can seem really lame. It's easy to confuse them and there's not much real-world application for these things. Textbooks try really hard to make it sound like there is...but they're a bunch of liars. The only applications I could find in my textbook (that weren't related to scientific notation) looked this like:
I don't think this is a bad problem. In fact, I like that it makes you think about area. But this isn't a real-world application because you'd never actually need to find the length of a rectangle like this. (Trust me. I was an engineer for six years. I never had to do anything like this.)
And kids pick up on that lameness. This is one of those lessons, up there with factoring polynomials and simplifying radicals, where students will at some point ask, "When will I ever use this?" This question usually comes up when a particular student is getting frustrated with the lesson and suddenly says to himself, "I don't get this. This is stupid and not worth my time. I'll probably never use this outside of school anyway."
And then we, the teachers, come up with a myriad of excuses: you need it for Algebra 2, you'll need it for the test, you'll need it when you're doing sciencey-kinds of things some day, you'll need it when you're flipping burgers at a rate of 2x^6/x^6 per minute, etc. None of these answers are satisfying to the students.
On top of all of this lameness, we make things worse by explicitly teaching students the rules for exponents. We don't give them the chance to figure them out on their own. I think there is a huge danger in just teaching students rules (or procedures or tricks). If you don't let students develop the meaning behind those rules and procedures, they are subject to error...like when a student tries to multiply two fractions, but for some reason he or she cross-multiplies. Or when they get really good with rise over run, and when you ask them to plot (4, 3), they move 4 up from the origin, and then over 3. Without meaning, rules and procedures become confused and are applied in the wrong situations.
Now, I always thought that I did a good job with teaching exponents. I always explained everything. I showed them how to expand expressions and put them back together.
The logic was there. The kids who were carefully listening "got it". But there were a lot of kids who only got the rule...just add the exponents.
As time went on, and I explained more and more of these rules, students became confused. They didn't really understand what was going on. They didn't know when to add or multiply exponents. They forgot that powers had to have the same base to combine them. They started to think that 2 times 3 was 5!
Here's a nice little graphic that shows how I feel when I teach exponents. You can see what happens as more and more rules get piled on. Students get confused and I'm left wondering, what happened? It was all going so well.
Some teachers are using a different approach. They're allowing students to discover the rules on their own. Just read these sweet posts by Andrew Stadel and Timon Piccini. (It's worth mentioning that both of these posts were inspired by Michael Pershan, who is doing a lot of awesome stuff himself.) I believe that exponents, like many things we teach, are a lot easier to understand if we de-emphasize the rules. And when students understand, they are less likely to ask, "When are we going to use this?", and they might actually enjoy mastering this concept.
Many times, we think we have to show our students every little step before they can do it on their own. Over the last few years, I've discovered that this really isn't the case. Don't believe me? Next time you teach something new, ask yourself if any of your students can figure it out without you explaining it to them. If you believe that at least one of your students can solve it without your help, let them try it. Just shut up, and let them work. Let them come to terms with what you're asking them to do. Let them wrestle with it a bit. Even if they don't get it, at least they're invested in the problem and they have some motivation to learn about its solution.
When you allow students to find their own solutions, they're going to appreciate it much more than you telling them how to do it...if only you'd shut up for once.
Here's the sequel to this post...."I Shall Never Play a Review Game Again!"
Admit it. For most students, exponent rules can seem really lame. It's easy to confuse them and there's not much real-world application for these things. Textbooks try really hard to make it sound like there is...but they're a bunch of liars. The only applications I could find in my textbook (that weren't related to scientific notation) looked this like:
I don't think this is a bad problem. In fact, I like that it makes you think about area. But this isn't a real-world application because you'd never actually need to find the length of a rectangle like this. (Trust me. I was an engineer for six years. I never had to do anything like this.)
And kids pick up on that lameness. This is one of those lessons, up there with factoring polynomials and simplifying radicals, where students will at some point ask, "When will I ever use this?" This question usually comes up when a particular student is getting frustrated with the lesson and suddenly says to himself, "I don't get this. This is stupid and not worth my time. I'll probably never use this outside of school anyway."
And then we, the teachers, come up with a myriad of excuses: you need it for Algebra 2, you'll need it for the test, you'll need it when you're doing sciencey-kinds of things some day, you'll need it when you're flipping burgers at a rate of 2x^6/x^6 per minute, etc. None of these answers are satisfying to the students.
On top of all of this lameness, we make things worse by explicitly teaching students the rules for exponents. We don't give them the chance to figure them out on their own. I think there is a huge danger in just teaching students rules (or procedures or tricks). If you don't let students develop the meaning behind those rules and procedures, they are subject to error...like when a student tries to multiply two fractions, but for some reason he or she cross-multiplies. Or when they get really good with rise over run, and when you ask them to plot (4, 3), they move 4 up from the origin, and then over 3. Without meaning, rules and procedures become confused and are applied in the wrong situations.
Now, I always thought that I did a good job with teaching exponents. I always explained everything. I showed them how to expand expressions and put them back together.
The logic was there. The kids who were carefully listening "got it". But there were a lot of kids who only got the rule...just add the exponents.
As time went on, and I explained more and more of these rules, students became confused. They didn't really understand what was going on. They didn't know when to add or multiply exponents. They forgot that powers had to have the same base to combine them. They started to think that 2 times 3 was 5!
Here's a nice little graphic that shows how I feel when I teach exponents. You can see what happens as more and more rules get piled on. Students get confused and I'm left wondering, what happened? It was all going so well.
Some teachers are using a different approach. They're allowing students to discover the rules on their own. Just read these sweet posts by Andrew Stadel and Timon Piccini. (It's worth mentioning that both of these posts were inspired by Michael Pershan, who is doing a lot of awesome stuff himself.) I believe that exponents, like many things we teach, are a lot easier to understand if we de-emphasize the rules. And when students understand, they are less likely to ask, "When are we going to use this?", and they might actually enjoy mastering this concept.
Many times, we think we have to show our students every little step before they can do it on their own. Over the last few years, I've discovered that this really isn't the case. Don't believe me? Next time you teach something new, ask yourself if any of your students can figure it out without you explaining it to them. If you believe that at least one of your students can solve it without your help, let them try it. Just shut up, and let them work. Let them come to terms with what you're asking them to do. Let them wrestle with it a bit. Even if they don't get it, at least they're invested in the problem and they have some motivation to learn about its solution.
When you allow students to find their own solutions, they're going to appreciate it much more than you telling them how to do it...if only you'd shut up for once.
Here's the sequel to this post...."I Shall Never Play a Review Game Again!"
Monday, May 13, 2013
A Better Way to Teach Area and Perimeter
I don't use a textbook for a number of reasons. Here's another one to add to the list....
I'm tired of how textbooks treat area and perimeter. For one thing, it's very formula-based, and I believe that strips away some of the thought processes when trying to understand these concepts. Take a look at this example on finding the area of a rectangle:
Now, I understand why you might give a formula for the area or volume of some shapes, but why on Earth would you give one for perimeter? You've just taken an idea that is really easy to understand and apply, and have made it much more difficult and subject to error. Students also lose the meaning of perimeter because they're not connecting the idea with the sum of the sides. They're just looking for the formula that begins with a P and cranking out an answer.
On top of that, textbooks and worksheets always conveniently give students the measurements.
I have two problems with this. For one, if I get an answer for area, I don't really have a way to check it. So my answer is 288 square meters. How do I know if I'm right...or even close? Is that answer reasonable? How would I know?
Second, people always complain that students are terrible at measurement. Then we give them tasks that are devoid of measuring. Why would we do that? It doesn't make sense. If there's an opportunity for your students to measure something in class, make them do it. How else do you expect them to get any good at it?
If you must use a worksheet, I would suggest it look more like this:
I'm tired of how textbooks treat area and perimeter. For one thing, it's very formula-based, and I believe that strips away some of the thought processes when trying to understand these concepts. Take a look at this example on finding the area of a rectangle:
Now, I understand why you might give a formula for the area or volume of some shapes, but why on Earth would you give one for perimeter? You've just taken an idea that is really easy to understand and apply, and have made it much more difficult and subject to error. Students also lose the meaning of perimeter because they're not connecting the idea with the sum of the sides. They're just looking for the formula that begins with a P and cranking out an answer.
On top of that, textbooks and worksheets always conveniently give students the measurements.
I have two problems with this. For one, if I get an answer for area, I don't really have a way to check it. So my answer is 288 square meters. How do I know if I'm right...or even close? Is that answer reasonable? How would I know?
Second, people always complain that students are terrible at measurement. Then we give them tasks that are devoid of measuring. Why would we do that? It doesn't make sense. If there's an opportunity for your students to measure something in class, make them do it. How else do you expect them to get any good at it?
If you must use a worksheet, I would suggest it look more like this:
It's not terribly exciting, but it accomplishes a couple of things.
1. There are no measurements listed. Students have to find their own measurements. They also have to think about which measurements are necessary...especially for area.
2. I print this out so that figure A is 1 square inch. With that, I can make guesses about the area of every other figure. I can check to make sure that my answer makes sense.
3. I can make comparisons between shapes. I can rank them in order of biggest to smallest. I can check to see that the sum of the areas of the shapes total the same area as the entire worksheet.
4. Students can compare answers, and once seeing that not everyone has the exact same answer, talk about error in measurement.
If you try this, let me know how it goes.
Sunday, May 12, 2013
Torturing Kids with Toothpicks - Part 2
I recently wrote a post on Dan Meyer's toothpick problem and mentioned something about a tough sequel I made for the kids. I was worried that the first question was too easy to solve and they really needed something a little more challenging.
So where did they struggle? Everywhere.
First, many weren't sure about how the triangle should be oriented. I saw several diagrams that looked like this::
So I asked them to determine how many toothpicks I would need to make as large a triangle I could on the floor of the classroom. Here is all of the important information I gave the kids:
My classroom is 30 feet by 20 feet.
That's it. And with that, my students had everything they needed to figure this out. Well...almost everything. They needed the length of a toothpick. I didn't give them this. But I did give them a handful of toothpicks and a ruler. They found the toothpicks to be 2.5 inches long.
So where did they struggle? Everywhere.
First, many weren't sure about how the triangle should be oriented. I saw several diagrams that looked like this::
I asked them how they knew that this would be the biggest triangle. After a lot of shrugs, I asked them to consider what would happen if I rotated the triangle so that it lay on the bottom of the rectangle:
And couldn't you then make that triangle bigger?
Then I went to another group. They wanted to know the distance across the room diagonally (from corner to corner). They wanted to measure it with a ruler, but this would have been a little distracting to the rest of the class. So I quickly grabbed a calculator, did a little Pythagorean Theorem, and said, "It's 39 feet." I cringed at the thought of what they were going to do with that information, but moved on to the next group.
This new group wanted to know the length from the corner to the midpoint of the opposite wall. Again, a little PT and..."It's 29 feet and 2 inches." I thought, that's not going to work. And they're going to hate me when they realize that I knew this wasn't going to work and didn't point it out to them.
Next, a girl asked me for masking tape. I had no idea what she was going to do with it, but it sounded exciting. So I said, "Yes! Tape! Coming right up! You're not going to use a lot, right? No? Great. Have at it." I walked away.
I come back to the other group who wanted the diagonal. Sure enough, they have this drawn on their paper:
So I ask, "What kind of triangle is that?" After some fumbling for answers, they come up with "right triangle". "Right, and what kind of triangle are we making?" Again, after some discussion, they realize that they need an equilateral triangle.
After receiving a few dirty looks, I moved on and checked in on the other group who wanted the midpoint.
I have a similar discussion with this group about how this isn't an equilateral triangle. I move on...
The girl who wanted the tape is making a 1 square foot box outline on the floor. She is asking for toothpicks to place within the box. I'm scratching my head at this point, still hopeful that this is going somewhere. I ask, "What are you going to do with this information?" She explains how she's going to use proportions to find the number of toothpicks in the large triangle. At first this sounded awesome, but then she started to talk about comparing the area of the small box to the entire room. I explained that this comparison may not be an equal proportion, and that she might be able to use this method by comparing areas of triangles instead. As cool as it would have been, this group eventually abandoned the proportion method.
The day goes on, and there are plenty of errors to correct. One group thinks that there are only 12 little triangles along the bottom of the big triangle. I asked them if that makes sense and I got the blank stares associated with the though process of "Crap. That doesn't make sense. I just wasted three minutes of my life doing this the wrong way." I asked them how they came up with 12...here's what they did:
30 feet / 2.5 inches = 12 toothpicks
Aaahhh! These are two different units of measurement! I pointed this out and moved on.
Another groups found that there are 144 little triangles along the bottom of the big triangle. And with this knowledge they attempted to find the number of triangles in the entire structure. They completely disregarded the 25 foot length of the room and didn't bother to check to see if the triangle would actually fit in that direction. I pointed this out and helped them see that the height of the large triangle was dependent on the height of one little triangle. And with that, the period was over....
The next day more groups got to this same point. But none of them knew how to find the height of this small triangle. Did they completely forget that I gave them toothpicks and rulers? Why didn't they think to measure it?
(It's probably important that I mention that these students have not had any exposure to the Pythagorean Theorem. That doesn't happen until 8th grade.)
I drew a triangle made of toothpicks on the board and pointed out that many of them have already found the length of a toothpick.
I asked them how they found the length of one toothpick. "We measured it." Right! So what's to stop you from putting some toothpicks together and measuring the height? Some heads started to nod, and after some assembling of toothpicks and measuring, we got a height.
Finally, they were getting close. They found the actual number of layers in the triangle and they started to calculate the number of little triangles. Problem is, there are a lot of layers...well over 100. And I know from experience that my kids are prone to making mistakes when they are making a lot of calculations. One missed button on the calculator ruins the whole thing. But I let it go, hoping someone would come up with a better way to do this.
The next day, I presented this problem on the board as a warm-up:
Students quickly realized that they just needed to add the numbers from 1 to 20.
And of course, they added them from left to right. But a few knew of a trick with the commutative property that would make it easier.
One explained how you could add the first and last number to get 21, then do the same thing with 2 and 19, 3 and 18, and so on, until you have ten sets of 21. Therefore, the answer is 10x21=210. (Supposedly, Gauss came up with this method as a kid in school. He sounds like an annoying little know-it-all.)
I gave the students the remaining class time and all weekend to finish their work. Tomorrow I get their solutions. Let's hope it all comes together.
This was a very difficult task, and at times, I regretted giving this to them. I was often worried that I didn't scaffold them enough ahead of time. But in the end, it all worked out Each step was something of a hurdle, and with a lot of good discussions, we somehow managed to get through it all.
You're still here? Great. I'm thinking about actually building this thing in my classroom. I went on amazon.com to order toothpicks, and apparently, I can choose between new and used toothpicks. How exciting!
Wednesday, May 8, 2013
Would adults use algebra? What if we give them Oreos?
In my recent post, "Teaching Algebra without algebra", I tried to build algebraic understanding in my students by comparing their intuitive solutions to algebraic ones. I began to wonder how the colleagues in my school would try to solve a similar problem. Would they simply reason their way through it, or would they actually use a system of equations?
So I proposed this problem to them which is completely stolen from Christopher Danielson. Anyone in the mathtwitterblogosphere is probably already familiar with it. Chris is well known within that community. And he made this video of his son which I'll never forget.
Here's the scenario:
My co-teacher, Mrs. Runkle, and I both love to eat Oreo cookies. She especially likes the ones called Double Stuf because they have twice the filling. She loves the filling....but she doesn't like the cookie wafers. They get in her teeth and she looks funny when she smiles. I'm the opposite. I can't get enough of the wafers, but the filling is disgusting. It looks like some kind of heavily processed glop that could double as an adhesive...maybe that's why it's called "Double Stuf". We came up with a solution. We agreed to buy a package of Double Stuf Oreos and share them. She would eat the filling off of each cookie, and then hand the remaining wafers to me to eat.
Note: I actually re-enacted this in a class with her. She scraped off the cream with her teeth, then I took the two cookies and ate them. She didn't know I was going to do that. The kids thought it was gross.
Then I tell the kids that Mrs. Runkle and I had an argument. We can't decide who is consuming more calories. I say the cream is made of stuff that is bad for you because it's mostly sugar and fat and who knows what, and therefore, has more calories. She thinks the two wafers are bigger than the filling and therefore, they have more calories. We look at the nutrition facts to see who is right, but it only says that two double stuff cookies have 140 calories. This didn't seem to help. Luckily, we had a package of regular Oreos, but that didn't help much either. All it told us was that three regular Oreos have 160 calories.
So...who's getting more calories? What can we do to figure this out?

I sent this out as an email to all of my co-workers for them to figure out. I told them that if they came up with a unique solution, they would get one Double Stuf Oreo. (Yeah, just one. I'm cheap.)
Here are some of their responses:
Solution 1 (5 people came up with this method):
160 calories divided by 3 cookies = 53.3 calories per regular cookie
140 calories divided by 2 cookies = 70 calories per Double stuff cookie……
70 – 53.3 calories = 16.7 more calories in a double stuff
16.7 x 2 (double stuff) = 33.4 calories in the double stuff stuffing alone
70 calories total – 33.4 calories in the double stuff stuffing (total) = 36.6 calories in the cookies.
The person who only eats the cookies consumes more calories. 3.2 calories
Solution 2 (1 person came up with this...believe it or not, this was not a math teacher):
3 Regular Oreos (R ) = 160Cal
2 Double Stuff Oreos (D) = 140Cal
R = 160/3
R = 53 1/3Cal
D = 140/2
D = 70Cal
If it is accepted that the components of a regular Oreo are cookies (C ) and filling (F)
AND
If it is accepted that the components of a Double Stuff Oreo are cookies (C ) and Double
filling (2F)
Then
R = C + F
D = C + 2F
Therefore the difference between a regular Oreo and a Double Stuff Oreo is a single serving
of filling (F):
D-R = (C+F)-(C+2F)
D-R = C + F – C – 2F = C + F – C – 2F
D-R=F
If D = 70 and R = 53 1/3:
AND
D-R = F
Then
F = 70 – 53 1/3
F = 16 2/3 calories
Since a Double Stuff Oreo contains 2F, the friend who eats only the cookies consumes:
2F = 2X(16 2/3)
2F = 33 2/3Calories per cookie
To find the calorie content of a Double Stuff Oreo Cookie, we need only to go back to the
equation (D = C+2F) and solve for C:
70 = C + 33 2/3
C = 70 – 33 2/3
C = 36 2/3 Calories
The cookie-eating friend consumes 36 2/3 calories per cookie.
The filling-eating friend consumes 33 1/3 calories per cookie.
Answer:
The friend who eats only the cookie part of the Double Stuff Oreo will consume 3 1/3 MORE
calories per cookie than the friend who eats only the filling part of the same cookie.
Solution 3 (again, not a math teacher - also, this person solved it using a system of equations and two different methods, elimination on the left and substitution on the right), 2 non-math and 1 math teacher used this method:

So about half of the responses used algebra...half didn't. While I think it's great that so many were eager to figure this out, I wonder why some would prefer to use an algebraic method. Did they do that because that's the most natural way for them to solve this problem? Was there something about the problem that tipped them off to think about using a system of equations? Or did they assume that the solution had to be an algebraic one because I teach Algebra?
And finally, can we really say if one solution is better than another? (And what do we mean by "better"?) I can see the benefits of doing it either way. For solution 1, you really have to be thinking about what's going on at each step. In solution 3, once you set it up, your hours and hours of practicing solving systems of equations take over and you don't need to worry about context anymore. You're on auto-pilot. Is that a good thing? And which way was more efficient? Solution one appears to take five calculations. Solution three has about 12. As an Algebra teacher, this concerns me.
Other thoughts:
1. A big thank you to Marshall Thompson for inspiring me to look into this! He also expressed interest in how people solve these problems differently.
He told me that someone once used this diagram as a solution. I love how simple this makes everything. It is basically using the same method as solution 1, but it practically screams a system of equations.

2. "Double Stuf"? Where the heck is the second "f"?
3. Here is an article about Stuf from The Onion.
4. The amazing Fawn Nguyen has made her own contribution. She actually saw this method first. She is nothing short of genius...or bizarre.
So I proposed this problem to them which is completely stolen from Christopher Danielson. Anyone in the mathtwitterblogosphere is probably already familiar with it. Chris is well known within that community. And he made this video of his son which I'll never forget.
Here's the scenario:
My co-teacher, Mrs. Runkle, and I both love to eat Oreo cookies. She especially likes the ones called Double Stuf because they have twice the filling. She loves the filling....but she doesn't like the cookie wafers. They get in her teeth and she looks funny when she smiles. I'm the opposite. I can't get enough of the wafers, but the filling is disgusting. It looks like some kind of heavily processed glop that could double as an adhesive...maybe that's why it's called "Double Stuf". We came up with a solution. We agreed to buy a package of Double Stuf Oreos and share them. She would eat the filling off of each cookie, and then hand the remaining wafers to me to eat.
Note: I actually re-enacted this in a class with her. She scraped off the cream with her teeth, then I took the two cookies and ate them. She didn't know I was going to do that. The kids thought it was gross.
Then I tell the kids that Mrs. Runkle and I had an argument. We can't decide who is consuming more calories. I say the cream is made of stuff that is bad for you because it's mostly sugar and fat and who knows what, and therefore, has more calories. She thinks the two wafers are bigger than the filling and therefore, they have more calories. We look at the nutrition facts to see who is right, but it only says that two double stuff cookies have 140 calories. This didn't seem to help. Luckily, we had a package of regular Oreos, but that didn't help much either. All it told us was that three regular Oreos have 160 calories.
So...who's getting more calories? What can we do to figure this out?

I sent this out as an email to all of my co-workers for them to figure out. I told them that if they came up with a unique solution, they would get one Double Stuf Oreo. (Yeah, just one. I'm cheap.)
Here are some of their responses:
Solution 1 (5 people came up with this method):
160 calories divided by 3 cookies = 53.3 calories per regular cookie
140 calories divided by 2 cookies = 70 calories per Double stuff cookie……
70 – 53.3 calories = 16.7 more calories in a double stuff
16.7 x 2 (double stuff) = 33.4 calories in the double stuff stuffing alone
70 calories total – 33.4 calories in the double stuff stuffing (total) = 36.6 calories in the cookies.
The person who only eats the cookies consumes more calories. 3.2 calories
Solution 2 (1 person came up with this...believe it or not, this was not a math teacher):
3 Regular Oreos (R ) = 160Cal
2 Double Stuff Oreos (D) = 140Cal
R = 160/3
R = 53 1/3Cal
D = 140/2
D = 70Cal
If it is accepted that the components of a regular Oreo are cookies (C ) and filling (F)
AND
If it is accepted that the components of a Double Stuff Oreo are cookies (C ) and Double
filling (2F)
Then
R = C + F
D = C + 2F
Therefore the difference between a regular Oreo and a Double Stuff Oreo is a single serving
of filling (F):
D-R = (C+F)-(C+2F)
D-R = C + F – C – 2F = C + F – C – 2F
D-R=F
If D = 70 and R = 53 1/3:
AND
D-R = F
Then
F = 70 – 53 1/3
F = 16 2/3 calories
Since a Double Stuff Oreo contains 2F, the friend who eats only the cookies consumes:
2F = 2X(16 2/3)
2F = 33 2/3Calories per cookie
To find the calorie content of a Double Stuff Oreo Cookie, we need only to go back to the
equation (D = C+2F) and solve for C:
70 = C + 33 2/3
C = 70 – 33 2/3
C = 36 2/3 Calories
The cookie-eating friend consumes 36 2/3 calories per cookie.
The filling-eating friend consumes 33 1/3 calories per cookie.
Answer:
The friend who eats only the cookie part of the Double Stuff Oreo will consume 3 1/3 MORE
calories per cookie than the friend who eats only the filling part of the same cookie.
Solution 3 (again, not a math teacher - also, this person solved it using a system of equations and two different methods, elimination on the left and substitution on the right), 2 non-math and 1 math teacher used this method:

So about half of the responses used algebra...half didn't. While I think it's great that so many were eager to figure this out, I wonder why some would prefer to use an algebraic method. Did they do that because that's the most natural way for them to solve this problem? Was there something about the problem that tipped them off to think about using a system of equations? Or did they assume that the solution had to be an algebraic one because I teach Algebra?
And finally, can we really say if one solution is better than another? (And what do we mean by "better"?) I can see the benefits of doing it either way. For solution 1, you really have to be thinking about what's going on at each step. In solution 3, once you set it up, your hours and hours of practicing solving systems of equations take over and you don't need to worry about context anymore. You're on auto-pilot. Is that a good thing? And which way was more efficient? Solution one appears to take five calculations. Solution three has about 12. As an Algebra teacher, this concerns me.
Other thoughts:
1. A big thank you to Marshall Thompson for inspiring me to look into this! He also expressed interest in how people solve these problems differently.
He told me that someone once used this diagram as a solution. I love how simple this makes everything. It is basically using the same method as solution 1, but it practically screams a system of equations.

2. "Double Stuf"? Where the heck is the second "f"?
3. Here is an article about Stuf from The Onion.
4. The amazing Fawn Nguyen has made her own contribution. She actually saw this method first. She is nothing short of genius...or bizarre.
Subscribe to:
Posts (Atom)